
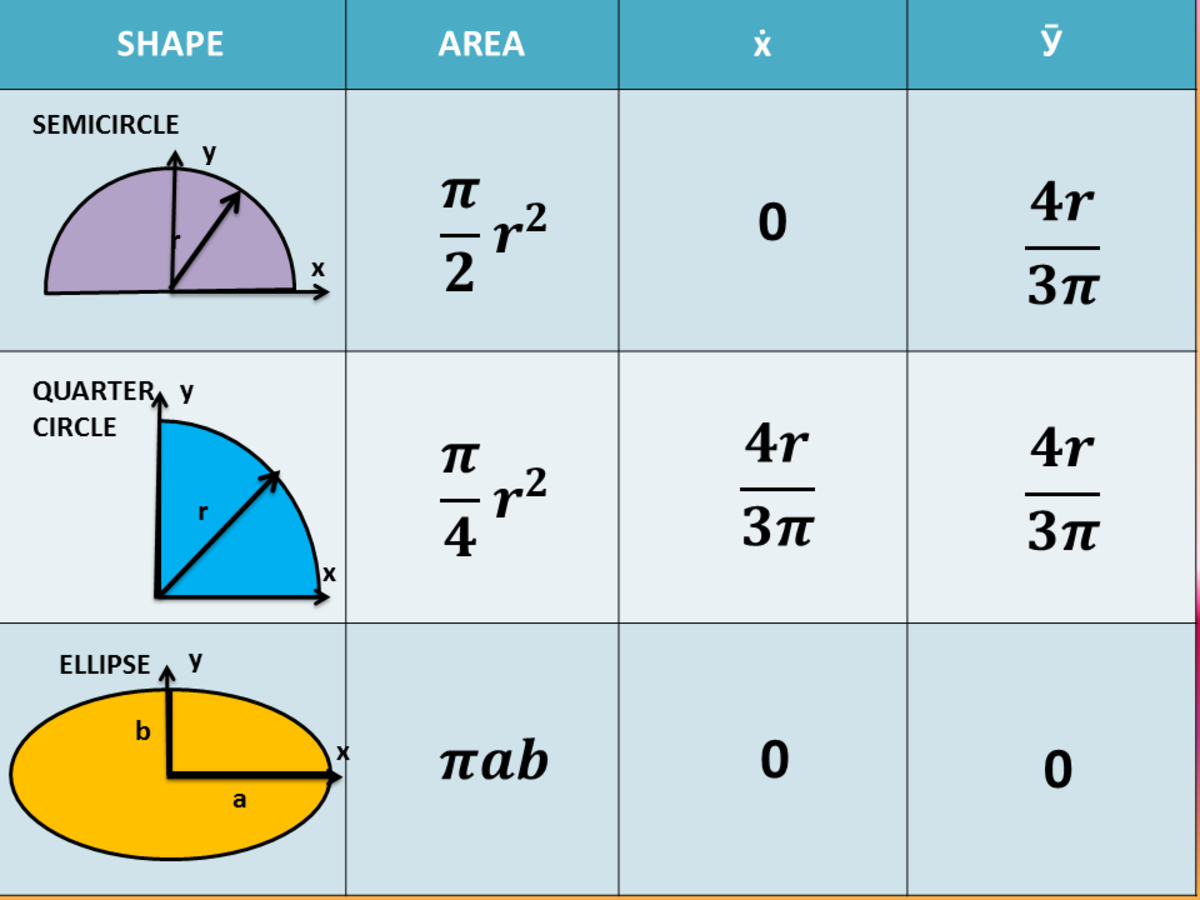
Point mass M at a distance r from the axis of rotation.Ī point mass does not have a moment of inertia around its own axis, but using the parallel axis theorem a moment of inertia around a distant axis of rotation is achieved. In general, the moment of inertia is a tensor, see below. This article mainly considers symmetric mass distributions, with constant density throughout the object, and the axis of rotation is taken to be through the center of mass unless otherwise specified.įollowing are scalar moments of inertia. When calculating moments of inertia, it is useful to remember that it is an additive function and exploit the parallel axis and perpendicular axis theorems. In general, it may not be straightforward to symbolically express the moment of inertia of shapes with more complicated mass distributions and lacking symmetry. Typically this occurs when the mass density is constant, but in some cases the density can vary throughout the object as well. The mass moment of inertia is often also known as the rotational inertia, and sometimes as the angular mass.įor simple objects with geometric symmetry, one can often determine the moment of inertia in an exact closed-form expression. It should not be confused with the second moment of area, which is used in beam calculations. Centroid of a Circle Arear2 A r e a r 2, Ix4r4 I x 4 r 4 Iy4r4 I y 4 r 4, Jz2r4. The moments of inertia of a mass have units of dimension ML 2( × 2). Centroids and Area Moments of Inertia for 2D Shapes Circle. 3 provides the moment of inertia and section modulus formula for common geometrical shapes.Moment of inertia, denoted by I, measures the extent to which an object resists rotational acceleration about a particular axis, it is the rotational analogue to mass (which determines an object's resistance to linear acceleration). In SI unit systems the unit of Section Modulus is m 3 and in the US unit system inches 3. When we represent this equation in terms of the circles diameter (D), it becomes I D4 / 64.
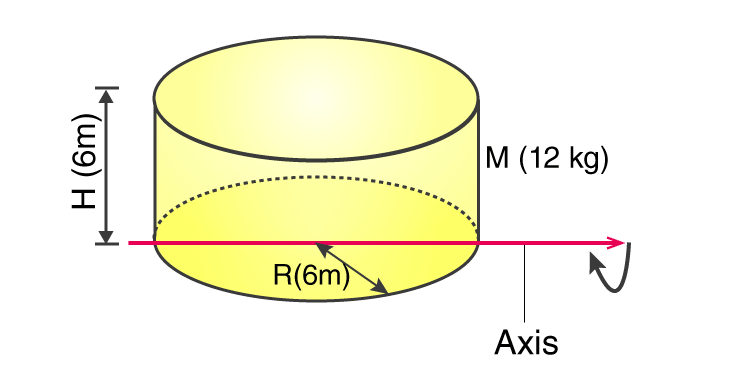
The radius is R, and the axis passes through the centre. Use the parallel axis theorem to find the moment of inertia of the circular ring about the \(y\) axis. The moment of inertia of a circle, also known as the second-moment area of a circle, is commonly calculated using the formula I R4 / 4. Section modulus is denoted by “Z” and mathematically expressed as Z=I/y The moment of inertia (MI) of a plane area about an axis normal to the plane is equal to the. The next example show how the parallel axis theorem is typically used to find the moment of inertia of a shape about an axis, by using then centroidal moment of inertia formulas found in Subsection 10.3.2. The section modulus of a section is defined as the ratio of the moment of inertia (I) to the distance (y) of extreme fiber from the neutral axis in that section. The larger the moment of inertia, the greater is the moment of resistance against bending. This equation is equivalent to I D 4 / 64 when we express it taking the diameter (D) of the circle. Bending stresses are inversely proportional to the Moment of Inertia. Moment of inertia of a circle or the second-moment area of a circle is usually determined using the following expression I R 4 / 4 Here, R is the radius and the axis is passing through the centre.

It tells you how much the object will resist rotational acceleration (usually called angular acceleration) for a given torque. The moment of inertia is the rotational equivalent to mass. Area moment of inertia is the property of a geometrical shape that helps in the calculation of stresses, bending, and deflection in beams. The moment of inertia (MI) of a plane area about an axis normal to the plane is equal to the sum of the moments of inertia about any two mutually perpendicular axes lying in the plane and passing through the given axis. Torque (or moment) is the rotational equivalent of force you apply it to cause an object to rotate to change rotational velocity.Mass moment of inertia provides a measure of an object’s resistance to change in the rotation direction.


 0 kommentar(er)
0 kommentar(er)
